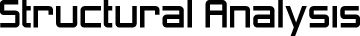動的破壊解析に関する研究

　構造物の破壊現象を評価することは社会性，公共性の高い構造物を扱う土木工学において非常に重要であると考えられます．特に近年，地震や土石流，津波などの自然災害に対する防災・減災の観点から社会的な関心も高まっています．
　そこで本研究では構造物の破壊現象を正確に評価するために，動的破壊解析手法の構築を行っています．現在は，主にコンクリートなどの準脆性材料に対するひび割れ進展解析を行っています．
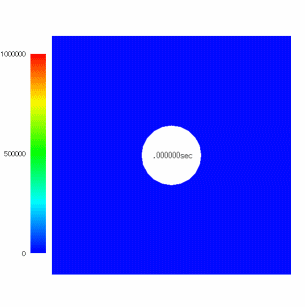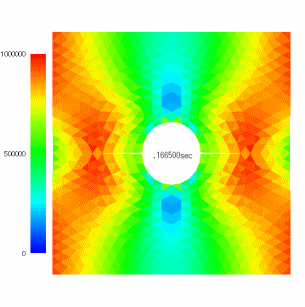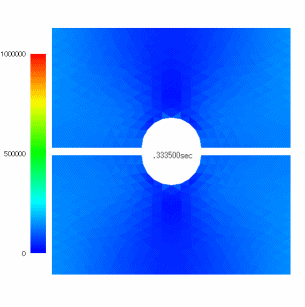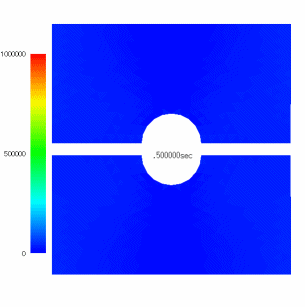
　　　　　　　　　　　　　　　　　　　 　　　　　□円孔穴あき板に対張破断解析



　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　
　　　　　　　　　　　　　　　□レンガ積み構造物に対する動的破壊解析





Euler型大変形固体解析に関する研究

　大変形を伴う固体の解析においては，物質点の大変位や回転に対して取り扱いが可能な解析手法が必要となります．固体力学の従来の定式化では，物質の変形に追従した観測点において変形を記述するLagrangian 解法が用いられます．しかしながら，大変形問題をLagrangian 解法で解析した際，計算格子が潰れ，計算精度の低下や計算が破綻することが問題として挙げられています．
　それに対して，空間に固定された観測点において変形を記述するEulerian 解法では，計算格子の極端な歪みによる計算精度の低下や計算の破綻を回避することができ，大変形を伴う固体の解析に有効な手段だと考えられます．以上の点から，Eulerian 有限要素法を用いた固体の大変形解析に関する研究を行っています．

　　　　　　　　　　　　　　　　　　　　　　　□棒の衝突解析



流体-構造連成解析に関する研究

　土石流によって流された岩石等の物体が堤防や橋脚に衝突し，甚大な被害を及ぼします．これらの問題を数値解析により評価するためには，流体と物体の挙動が相関する流体-構造連成問題を，さらに時々刻々と複雑に変化する自由表面形状と移動する物体を考慮した解析を行う必要があります．これらの移動境界面の取り扱い方法として，界面追跡法に基づく方法は，これらの界面を解析メッシュの境界として直接的に取り扱うため，界面を精度良く評価することのできる手法であります．しかしながら，これらの手法は移動境界を初期の解析メッシュで表現するため，大変形を伴う自由表面形状や構造物の大移動を伴った場合，解析メッシュの破綻により，解析を進めることができなくなってしまいます．
　その問題点を克服するために，バックグラウンドメッシュに基づくメッシュ再構築手法を導入した界面追跡法に基づく流体構造連成解析手法が提案します．